2. Теория парусных установок
2.1 Пластина в воздушном потоке
Чуть ли не всем пытливым изобретателям первым делом приходит на ум идея использовать не сложный в изготовлении пропеллер, а матерчатый парус или жесткий лист, который в рабочем цикле движется, увлекаемый ветром, а в холостой цикл возвращается в исходное положение, имея минимальное сопротивление ветру. Изобретатели, увлеченные идеей, начинают заниматься конструированием самой установки, ее механики и преодолением возникающих при решении этой задачи технических сложностей. Но реальность такова, что потраченные усилия чаще всего оборачиваются пустой тратой времени. Парусные ветроустановки, давайте обобщенно назовем их так, имеют низкий КИЭВ – коэффициент использования энергии ветра. Этот вывод следует из простых расчетов.
Давайте на валу электрогенератора закрепим барабан, на барабан намотаем трос от пластины (паруса) и попробуем добиться максимальной мощности от этой установки, изменяя скорость движения пластины.
Если пластина неподвижна и перпендикулярна скорости ветра, то на нее действует сила
Где:
F – сила давления воздушного потока [н],
Сx – коэффициент сопротивления, зависящий от формы тела,
р – плотность воздуха 1,29 [кг/м 3],
S – площадь поперечного сечения пластины [м 2]
Vв – скорость потока воздуха [м/с].
Коэффициент Cx зависит от формы тела. Понятно, что скорлупка, обращенная отверстием навстречу потоку, имеет большее сопротивление, чем та же скорлупка, обращенная выпуклостью к потоку. Самым же обтекаемым будет каплеобразная форма тела, обращенная тупым, а не острым, как ни странно, концом к потоку. Значения коэффициентов Cx для некоторых тел приведены ниже.
- Тонкая пластина перпендикулярная потоку Cx =1,11 – для небольших пластин и Cx = 1,33 для больших пластин
- Полусфера, отверстие обращено навстречу потоку (парашют) Cx=1,33
- Полусфера, отверстие обращено по потоку Cx =0,35
- Тело обтекаемой каплеобразной формы Cx =0,05
* Надо заметить к этой небольшой табличке, что в литературе по авиации коэффициент Сx вы можете встретить в расчетах часто другой, ровно в два раза меньший, что б была возможность не писать в формулах двойку в знаменателе.
Когда пластина движется, то она как бы убегает от ветра и относительная скорость воздушного потока, набегающего на пластину, снижается. Поэтому сила напора воздушного потока также будет меньше
Мощность равняется произведению силы на скорость
N= FV п (2.1.3)
Обратите внимание, что в этой формуле стоит не скорость ветра, а скорость перемещения пластины.
Мощность, получаемая на генераторе, составит
Если пластина неподвижна, то полезная мощность равна нулю. Если пластина движется со скоростью ветра, то она не испытывает давления и мощность тоже равна нулю. Для нахождения наивыгоднейшей скорости пластины, напишем формулу для КИЭВ. КИЭВ равен отношению полезной мощности к полной мощности ветрового потока.
Обозначим 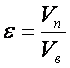 , тогда
, тогда
Чтобы найти, при каком значении e КИЭВ достигает максимума, надо продифференцировать 2.1.5 и приравнять полученное выражение к нулю, т.е. выполнить обычную в дифференциальном исчислении операцию нахождения максимума. В результате этих преобразований получим
Т.е. для достижения максимального КИЭВскорость пластины должна быть в три раза меньше скорости ветра.
Подставив полученное значение в 2.5, получим
ηмакс. = 0,148 Cx
Для плоской пластины КИЭВ равен 0,164 – 0,197.
Для полусферы с отверстием навстречу ветру КИЭВ равен 0,197
Теория в данном случае неумолима. Парусные конструкции имеют КИЭВ около 0,15, т.е. в три раза ниже, чем у пропеллера.
| Форма
паруса |
Отношение скорости паруса к скорости ветра e | ||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | ||
| Вогнутый
парус Cx = 1,33 |
0,108 | 0,170 | 0,196 | 0,192 | 0,166 | 0,128 | 0,084 | 0,043 | 0,012 | 0 | |
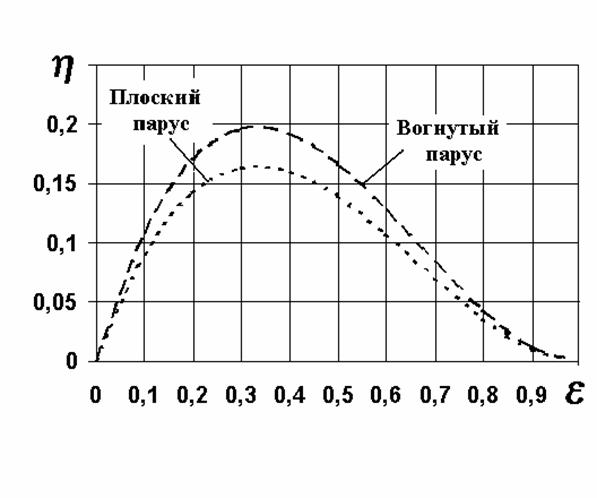
Таблица 2.1 Зависимость теоретически достижимого КИЭВ от скорости паруса.
Рис. 2.2 Зависимость теоретически достижимого КИЭВ от скорости паруса.
Совершив рабочий ход, пластина должна вернуться в исходную позицию, двигаясь против ветра. На обратном пути скорость пластины складывается со скоростью набегающего потока. Чтобы уменьшить потери, парус поворачивают ребром и придают ему обтекаемую форму. Мощность, которую потребуется приложить, чтобы возвратить пластину в исходную позицию, составит.
Где:
N2 – мощность необходимая для возврата пластины [Вт],
Сx – коэффициент сопротивления, зависящий от формы тела,
p – плотность воздуха 1,29 [кг/м 3],
S2 – площадь поперечного сечения пластины на обратном пути [м 2],
Vв – скорость ветра [м/с]
Vп2 – скорость пластины на обратном пути.
Можно написать эту формулу по-другому, обозначив 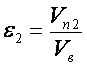
В формуле вместо КИЭВ появился коэффициент мощности h2 показывающий, какую часть от мощности ветра составляет мощность, затрачиваемая на перемещение тела против ветра. Отношение e 2 может составлять величину и больше единицы в отличие от e.
| Форма паруса | Отношение скорости паруса к скорости ветра e 2 | ||||||||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | |||
| Выпуклый
парус C x = 0,35 |
0,04 | 0,10 | 0,18 | 0,27 | 0,39 | 0,54 | 0,71 | 0,91 | 1,14 | 1,40 | 1,70 | 2,03 | 2,41 | 2,82 | 3,28 | ||
Табл. 2.2 Зависимость h2 от скорости паруса на обратном пути.
В предыдущем параграфе мы определили, что диаметр пропеллера ветряка должен быть не менее 10 метров, т.е. площадь, ометаемая лопастями, составит 78,5 м2. Для парусной установки площадь парусов при той же мощности составит 235,5 м2. Если паруса будут квадратными, то их размер должен быть 15,3 на 15,3 метра (100 листов фанеры на каждый парус). При круглых парусах их диаметр необходим 17,3 метра (диаметр парашюта около 20 метров).
В заключение этого параграфа подсчитаем на сколько повысится давление на поверхности паруса по сравнению с атмосферным. Мы уже говорили, что сила, воздействующая на парус равна
Давление же есть сила, приходящаяся на единицу площади
При скорости ветра 5 м/с и скорости пластины в одну треть от скорости ветра давление равно 9 паскалей. Напомню, что атмосферное давление, которое раньше измерялось в атмосферах, сейчас измеряется в паскалях. 1ат =101 325 Па. Т.е. давление на парус или лопасти ветряка при скорости ветра 5 м/с составит всего 0,0001 атмосферы. Вот такая неожиданно малая величина перепада давлений заставляет двигаться ветровые установки. На самом же деле формула 2.8 дает не давление на пластину с передней стороны, обращенной к ветру, а дает разницу давлений на передней и задней сторонах. На передней стороне пластины в нашем примере будет избыток давления примерно в 6 Па, а на задней – разряжение в 3 Па.
2.2 Чашечный анемометр
Теперь у нас достаточно выкладок, чтобы прикинуть эффективность устройств наподобие анемометра.
Для облегчения вычислений упростим задачу. Допустим, что во время рабочего хода чашечка все время перпендикулярна потоку, затем резко поворачивается тыльной стороной и совершает обратный ход тоже перпендикулярно потоку. Скорость движения равна оптимальной скорости 0,33 Vв . Т.е. фактически мы рассмотрим «гусеничный» анемометр.
Мощность, затрачиваемая на обратный ход, будет равна
Для чашки, движущейся выпуклостью вперед, Cx2 =0,35. Коэффициент мощности во время обратного хода составит 0,21. А во время рабочего хода достигаемая мощность, как мы подсчитали ранее, равна только 0,197 полной мощности ветра. Т.е. мощность, требуемая на обратный ход, получается больше, чем при рабочем ходе. Анемометр с такими характеристиками будет не давать, а поглощать энергию.
Почему получается такой результат?
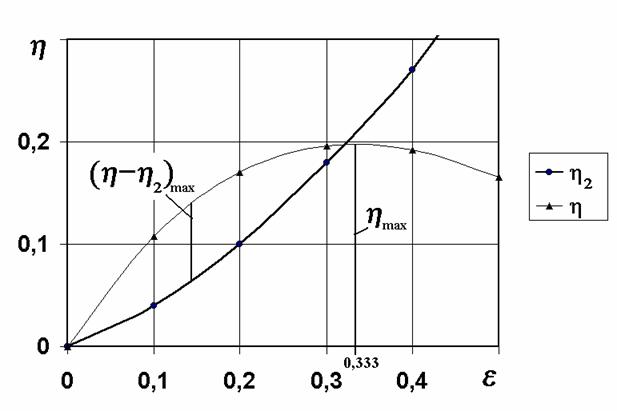
Рис. 2.2. Графики h и h2 для анемометра.
Во время рабочего хода скорость набегания потока на пластину равна 0,67 Vв , а на обратном пути 1,33 Vв , т.е. в два раза больше. Мощность, тормозящая тело, пропорциональна квадрату скорости набегания воздуха. (Не квадрату скорости движения, а квадрату относительной скорости воздуха и пластины). Потребляемая мощность резко растет с увеличением скорости обратного хода. Поэтому скорость чашечки равная одной трети скорости ветра для анемометра недостижима.
Можно подсчитать, что если анемометр вращается без нагрузки, то его скорость составит 0,32 от скорости ветра. При такой скорости мощность за рабочий ход будет равна мощности затрачиваемой на обратный путь. Это видно на рисунке 2.2. Линии графиков h и h2 пересекаются при e, равном 0,32.
Если же по принципу анемометра сделать ветродвигатель, то для достижения максимальной полезной мощности скорость чашечек необходимо уменьшить до 0,16V в (вместо оптимальной скорости 0,33V в паруса, который не совершает обратного хода). Тогда мощность за рабочий ход упадет процентов на тридцать от теоретически достижимой для рабочего хода, но одновременно и мощность, требуемая на холостой ход, уменьшится в два раза. Общий баланс станет положительным. КИЭВ достигнет величины 0,075. Или 7,5% от полной энергии ветра. Этот вывод объясняет низкий КИЭВ у виндротора и подобных установок с нескладывающимся на обратном пути парусом.
Оптимальной скорости добиваются правильным подбором нагрузки. Из графика 1.2 видно, что в довольно широком диапазоне e от 0,1 до 0,2 графики h и h2 идут почти параллельно, расстояние между ними мало меняется. Мощность, отдаваемая ветряком в этом диапазоне скоростей, остается приблизительно постоянной. Поэтому в домашней практике применения ветряк, оптимизированный под скорость ветра в 5 м/с, будет удовлетворительно работать и в диапазоне от 3,5 до 6,5 м/с. Большие, коммерческие агрегаты, оптимизируют более тщательно. Там борьба идет за каждый процент дополнительной мощности.
Те же результаты можно получить и аналитически. Приравняв 2.1.4 и 2.1.7 можно получить скорость движения анемометра без нагрузки
Если же мощности прямого и обратного хода вычесть и найти максимум, то получим, что ![]() =0,156, т.е. скорость при которой КИЭВ достигает максимума.
=0,156, т.е. скорость при которой КИЭВ достигает максимума.
Оценим скорость вращения ветроустановки, выполненной по принципу анемометра. При скорости ветра 5 м/с, окружная скорость подобной ветроустановки составит 0,156 Vв =0,75м/с . Поэтому ветроустановка выполненная по принципу анемометра будет делать десятка полтора оборотов в минуту. Для привода обычных генераторов потребуется мультипликатор со стократным увеличением скорости вращения.
Показатели реального, вращающегося измерительного анемометра будут примерно такими же как и у подсчитанного гусеничного анемометра. Чашечки во время рабочего хода расположены большую часть времени не перпендикулярно, а под углом к ветру, они становятся более обтекаемыми. Поэтому сила, воздействующая на них, а значит и скорость уменьшается. На обратном пути чашечки, поворачиваясь под углом, испытывают большее сопротивление, что также уменьшает скорость. Но, когда чашечки становятся ребром к ветру, на них действует за счет их выпуклости «подъемная» сила, направленная попутно, аналогичная силе, действующей на крыло самолета. Суммарный баланс этих противоположных влияний компенсируется и обеспечивает окружную скорость движения чашечек равную примерно 0,3 скорости ветра.
Карусельный ветродвигатель Нухова
Ветродвигатель Чебышева (Предшественник Савониуса)
Советский Савониус
Барабанный ветродвигатель

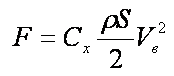
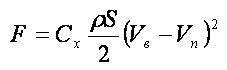
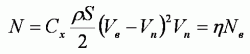
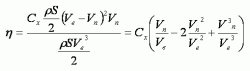
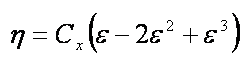
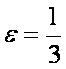
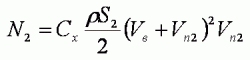
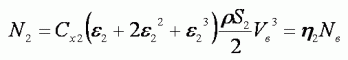
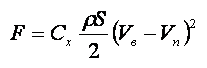
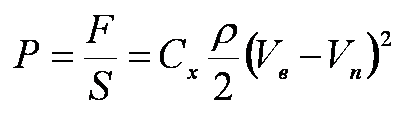
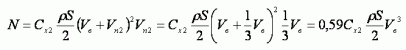
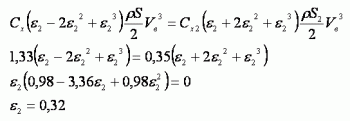





НЕ ОТКРЫВАЮТСЯ РИСУНКИ В “ТЕОРИЯ ПАРУСНЫХ УСТАНОВОК”. ЧТО НУЖНО СДЕЛАТЬ?