Вопросы по расчету лопастей

Ветер 8м/с, лопасти подвернуты на быстроходность4, обороты теже, момент вырос, мощность соответствует диаметру и скорости ветра. Дальше надо или сильно уширять лопасти или их количество? Я правильно понял?

Не будем завбывать, что мы говорим дальше о системе с постоянными оборотами ветряка, т.е. с постоянной окружной скоростью. Постоянные обороты обеспечиваются поворотом лопастей.

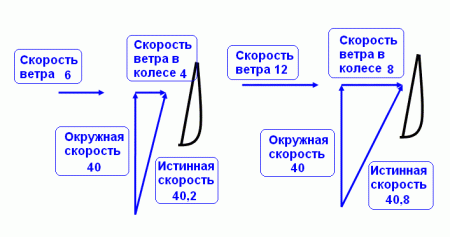
Представьте Вы сидите в машине, и снег бьет прямо в БОКОВОЕ стекло. Скорсть ветра 6 м/с. Но перед стеклом снежинки затормаживаются и бьют в стекло со скоростью 4 м/с. Вы поехали со скоростью 40 м/с ( 144 км/час). И снежинки начали бить по БОКОВОМУ стеклу наискосок под углом 5,7^о. Быстроходность Z = 6,7. Их скорость набегания (истинная скорость) считается как гипотенуза этого треугольника и равна 40,2 м/с. Если скорость ветра увеличилась до 12 м/с (8 м/с – подлет к стеклу), то истинная скорость 40,8 м/с, угол 11,3 градуса. Быстроходность Z =3,3. Т.е. истинная скорость практически не изменяется, она определяется только скоростью автомобиля.

Точно так же в ветряке. Окружная скорость лопастей неизменна и намного выше скорости ветра. Поэтому скорость набегания потока (истинная скорость) меняется мало при значительном росте ветра. Но сильно меняется угол.

Вы может сказать, что мощность растет в кубе от скорости. Мощность идеального или реального ветряка так и растет. Но здесь мы начинаем ему мешать. Поэтому надо взглянуть на процессы поближе.

Мощность есть произведение окружной скорости на окружную силу. Окружная скорость у нас неизменна. Силу можно определить только по векторам. Дальше смотрите вектора. Без векторов не объяснишь.

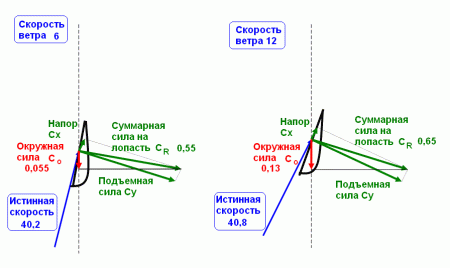
Зеленая подъемная сила перпендикулярна синей истинной скорости. Подъемная сила плюс сила напора образуют полную аэродинамическую силу. Лопасть движется не по направлению аэродинмической силы, а по окружности вращения. Поэтому ее движет проекция полной аэродинамической силы – красная окружная сила.

Ветер усилился, вектор полной силы повернулся, и Красная окружная сила увеличилась в два раза за счет поворота. Но и сам вектор подрос от 0,55 до 0,65 (это надо объяснять по полярам). Красный вектор стал 0,13.

Но это не сила, а только аэродинамический коэффициент. Его надо умножить на плотность воздуха, на площадь элемента крыла, на истинную скорость в квадрате и разделить пополам.

Истинная скорость возросла от 40,2 до 40,8, в 1,01 раза, а ее квадрат в 1,03 раза. Сила на элементе лопасти составит 1,03*0,13 = 0,134 , а раньше была 0,055. Т.е. суммарное увеличение силы, а значит и увеличение мощности (раз окружная скорость неизменна) 0,134/0,055 = 2,4 раза.

А ветер усилился в два раза, его мощность увеличилась в 8 раз. У нас будет огромный недобор мощности, если мы лопасти сделаем под малый ветер. Поэтому лопасти надо проектировать под тот ветер, с которого мы хотим начать ограничение мощности. Под 8 м/с.

Для 4 м/с эти лопасти будут чересчур широкие. Поэтому на 4 м/с ветряк вынужден будет сбросить обороты. А обороты мы как раз собираемся поддерживать неизменными. Значит надо либо недобирать мощность, либо выходить из положения за счет варьирования крутки по длине лопасти… Может еще какие варианты возникнут. Я не просчитывал этот вопрос. Надо составлять программу.

Самый простой способ – это просто поддерживать обороты недобором мощности. В этом способе есть тоже смысл. Основную долю энергии мы получаем на 5 м/с. Допустим 500 Вт. Изредка дует 8 м/с. Мы могли бы получать от этого ветра 2 кВт. Но есть ли смысл делать или покупать дорогой генератор, который только изредка будет включаться на полную мощность? Можно просто потерять мощность при повороте лопастей и получить 1 кВт на больших ветрах.

И в заключение. На рисунках показан только кончик лопасти. В середине лопасти быстроходность будет в два раза меньше. Поэтому угол истинного ветра будет больше. При увеличении скорости этот угол возрастет уже не в два раза, как на кончике лопасти. И все остальные цифры будут другие. Поэтому тут главное – надо понимать причины, а считать должен компьютер по программе. Конечно, можно попробовать загнать интегралы в Математику и получить аналитическое выражение, но боюсь, что будет слишком ненаглядно, и проще просчитать разные варианты. И остановиться на подходящем.

Количество лопастей находим по формуле; Кол. Лопастей (В) = 80/ TSR в квадрате. Берем к примеру быстроходность 3. В=80/3*3=8,8. Это означает, что винт с 8 лопастями можно сделать с быстроходностью не выше Z=3.

Эта формула появилась у Пигота вот откуда. Он выводит ее в предположении, что лопасть на конце имеет размер в 7% от радиуса ветряка. А почему именно так? Скорее всего, он для удобства счета принимает средний размер лопасти в 10% от радиуса. Но лопасть логично сделать зауженой к концу, расширенной к ступице. (Лучше стартует и уменьшается индуктивное сопротивление). Отсюда появляется 7 % на конце лопасти и 14% у ступицы.

Количество лопастей по Пиготу равно:

i = (16PiR)/(9Z²b)

где b – ширина лопасти на конце.

Подставьте сюда ширину лопасти равной 0,07R и вы получите ту формулу, что приводит Валера.

А эта формула появляется в свою очередь за счет того, что силу лобового сопротивления приняли равной нулю. Посмотрите по векторам, что я рисовал. Там проекция напора на окружную скорость примерно равна красной стрелке. (Для желобков) Т.е. такое допущение дает ошибку в два раза при вычислении ширины лопасти. И кроме того он принимает для простоты Сy равным единице. Реальный разброс на самом деле от 0,7 для желобков до 1,5 для хороших профилей. Поэтому суммарная ширина всех лопастей, вычисленная с учетом этих допущений может гулять в три!!! раза. Это суммарная ширина. Он эту суммарную ширину делит на стандартные отрезки, равнее 0,07R. И отсюда получает число лопастей i.

На самом деле эта формула связывает не количество лопастей с быстроходностью, а коэффициент заполнения колеса с быстроходностью. ib – это суммарная ширина всех лопастей. ib/DPi – это коэффициент заполнения. Он равен из той же формулы.

ib/DPi = 8/9Z² = 1/ Z ²

Посмотрите на парусные агрегаты из Челябинска и ветряки из сайта windmission. У них равное количество лопастей. Значит и равная должна быть быстроходность, если судить по формуле? Да нет, конечно. Потому что у них совершенно полярный коэффициент заполнения. В парусном ветряке коэффициент заполнения равен, допустим, 0,9 поэтому по последней формуле Z = 1,05, а в тонколепестковом ветряке коэффициент заполнения, около 0.12 поэтому Z = 2,7. Это больше походит на правду.

На 2 рис колесо WINDFLOWER имеет быстроходность 3.6.

Я это посчитал в предположении, что Cy = 1, что мы пренебрегаем Cx, и.т.д. Коэффициент заполнения я определил вообще на глаз… Просто, чтобы была ясна общая тенденция.

В расчете Пигота есть и другие допущения. Поэтому картина плывет еще больше. Но пользоваться его расчетом можно. Если и будет ошибка, то необходимая крутка все равно будет в лопастях обеспечена. А ошибку ветряк сам скомпенсирует вращаясь раза в 1,5 быстее или раза в 1,5 медленнее. При таком увеличении произойдет изменение углов во всех сечениях в одну сторону и ошибка более менее скомпенсируется и для кончика и для середины. Ну а комлевая часть – она вообще энергии не дает при вращении. Комлевая часть служит только для стартования.

Чтобы привести полный и достаточно достоверный расчет нужны очень обширные исследования. Данные производители и разработчики, разумеется, скрывают за грифом «ДСП». Так что методика в общих чертах понятна. Но дело стоит за экспериментальными данными.

Вот еще с Рейнольдсом не все понятно.
ЧИСЛО РЕЙНОЛЬДСА = 68 500 х ДЛИНА ХОРДЫ (м) х ИСТИННАЯ СКОРОСТЬ (м/с)
Получается, что если возмем хорду на конце предположем 0,1м. И при одной быстроходности на одинаковой скорости ветра Рейнольдс не будет зависеть от диаметра колеса при неизменной хорде? И если с увеличением числом Рейнольдса по эпюрам падает подъемная сила, то шире какой-то величины хорды при определенной быстроходности брать нельзя? И значит этот профиль годится только для тихоходных колес, где Рейнольдс будет в пределах 110000 или малых диаметров?

Все логично, но одно обстоятельство перечеркивает эту логику. Не надо забывать, что с увеличением диаметра колеса кончик лопасти очерчивает большее кольцо в воздухе. Кончик собирает ветродань с большей площади. Мощность – есть произведение окружной силы на окружную скорость. Окружная скорость у нас одинакова. Потому что мы ограничены быстроходностью в пределах 5 – 8. А сила, она равна аэродинамическому коэффиценту ( в данном случае красный вектор Сокр.) умножить на плотность, на площадь, на истинную скорость в квадрате разделить пополам. В этой формуле нечего увеличивать кроме площади. Т.е. хорды. Поэтому при увеличении диаметра ветряка растет ширина лопасти. Еще раз повторю. Ширину лопасти мы увеличиваем, чтобы собрать возросшую мощность. Поэтому у больших ветряков с увеличением хорды ВОЗРАСТАЕТ число Рейнольдса.

И если с увеличением числом Рейнольдса по эпюрам падает подъемная сила, то шире какой-то величины хорды при определенной быстроходности брать нельзя? И значит этот профиль годится только для тихоходных колес, где Рейнольдс будет в пределах 110000 или малых диаметров?

Ветряк двигает не подъемная сила, а проекция этой силы на плоскость вращения минус лобовое сопротивление. То есть красный вектор окружной скорости. Неважно, что будет с подъемной силой. Важно, что при увеличении числа Реейнольдса поляра сдвигается влево. Это позволяет увеличить быстроходность.

Там дальше Александр Николаевич рассматривает этот вопрос с точки зрения аэродинамического качества, т.е. отношения Cy/Cx. Этот подход даст более достоверный результат. В ветряках надо понимать такую вещь, что коэффициент окружной силы, или аэродинмическое качество, как мы его бы ни оптимизировали, не поможет увеличить мощность ветряка. Мощность ветряка определяется ветром. Быстроходность мы можем выжать из ветряка до предела с помощью расчетов, когда научимся считать. А если не нужна супер быстроходность, то можно задаться любой быстроходностью по рекомендации Пигота и получить ту же мощность, но на меньших оборотах и с более широкими лопастями.

i = (16PiR)/(9Z2b)

Михаил Николаевич, вы не потеряли Cl? В его формуле коэффициет подъемной силы присутствует и равен 0.8

В нашей отечественной авиационной науке коэффициент подъемной силы называется Сy. Авиацию 20 лет душат отсутствием финансирования, но в части военной авиации она остается передовой. Нет нужды переходить на заморский сленг. Нам нечего КАРДИНАЛЬНО менять в нашей аэродинамике. Я думаю, что авиаторы болезненно воспринимают попытки перевести терминологию на американские лапти. Их и так уже поставили на колени двадцатилетним отсутствием финансирования, зачем их еще задевать таким способом. Слов нет, американская аэродимика – сильная аэродинамика. Но не забывайте, что с 73 года ее успех в большей степени определяется печатанием ничем не обеспеченных денег. Нам надо не топтать собственную науку, а бережно лелеять ее и поддерживать. К сожалению, в российском интернете нет теории ветряков, приходится пользоваться пока зарубежными источниками. И книг подробных я тоже не втретил. Я этим начал заниматься три года назад. Исписал несколько тетрадей. И пришел к тем же примерно формулам, что дает и Пигот, только обросшими дополнительными уточнениями. Настанет время и на нас будут ссылаться. На Украину, Латвию, неважно. Нам есть что сказать. Мы равные с другими, а не меньшие братья.

Пегот в своем ПДФ в этой формуле ее тоже потерял(ошибочка).

На 6 странице он пишет: ПРЕНЕБРЕГАЯ СИЛОЙ ЛОБОВОГО СОПРОТИВЛЕНИЯ …

ДЛЯ ПРОСТОТЫ МЫ ПРЕДПОЛОЖИЛИ, ЧТО Сy = 1

Его фамилия не Пегот, а Пигот. Я его спрашивал, он объяснил так:

Like the animal “pig” and then “ott” just the same at “of” (or “on”)

but with t instead of f (or n).

Хотя, я не знаю английский, поэтому спросил у кого-то, как понимать написанное. Мне сказали, что он объясняет “Пигот”, поправльте, если не так.

И в своей програме расчета тоже присутствует.

Хорда = 16*пи* R( R/ r)/9* TSRв квадрате* B* Cl B кол. Лопастей Cl =0.8

Да и считает он для профиля кларк игрек. И угол альфа берет 4 градуса.

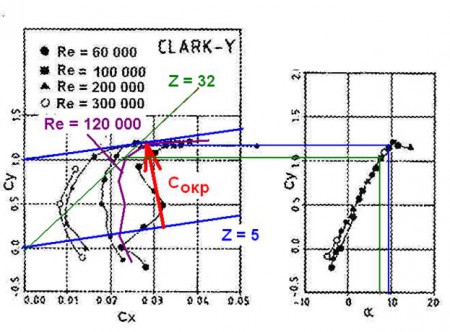
Давайте посмотрим и разберемся вместе. На рисунке я привел поляры для Clark- Y, которые дает Пигот. Проводим дополнительную поляру для Re = 120 000 фиолетовым цветом. Примерно, на глаз. Проводим к ней зеленую касательную и по другому графику находим угол альфа 7 градусов. Почему 7, а не 4, как Вы говорите? Скорее всего в том расчете, о котором Вы говорите он провел касательную к поляре для Re = 300 000 и получил 4 градуса. Не суть.

Если мы подсчитаем быстроходность для этой линии, то получим Z = 0,67 Cy/ Cx = 32. Почему такая нереальная цифра? Тут несколько причин. Две я объясню, с остальными не разобрался пока.

Во-первых, он не учитывает индуктивное сопротивление. Т.е. дополнительные потери для крыла КОНЕЧНОГО РАЗМАХА, как это называется в авиации. Замечали, что у планеров крылья длинные? Это для уменьшения индуктивных потерь. С учетом индуктивных потерь эта цифра быстроходности снизится в несколько раз. Те поляры, что он приводит, называются полярами ПРОФИЛЕЙ. Поляры, пересчитанные для учета индуктивного сопротивления, называются полярами КРЫЛЬЕВ или ЛОПАСТЕЙ. И остальные аэродинамические величины, надо внимательно смотреть по тексту. Аэродинамическое качество, допустим, чего? Профиля или крыла. Это разные вещи.

Во-вторых, зеленая касательная, которую он проводит определяет режим холостого хода для рекордной вертустановки по скорости. Если задаться целью построить пропеллер с максимально возможной скоростью на холостом ходу, то надо строить по зеленой линии и альфа отнимать, как он рекомендует 5 градусов. Если построить ветряк по такому проекту, то он просто снизит скорость ниже расчетной и будет давать мощнотсь. Но углы и ширина лопасти уже будут неоптимальны. Для оптимального рабочего режима надо задаться быстроходностью, допустим, Z = 5 и провести фиолетовую линию из начала координат. Проводят ее так. надо задаться любым значением Cx, допустим 0,025 и найти Cy = 1,5 ZCx = 0,18. И через точку с этими координатами и начало координат провести линию. Затем эту линию параллельно самой себе перенести выше, чтобы она коснулась поляры. Расстояние между этими линиями – будет окружной аэродинамический коэффициент Co. Я нарисовал его красным вектором. Расстояние по ПЕРПЕНДИКУЛЯРУ, а не по оси Y. (На этом графике построение неправильное. Надо чтобы масштаб по осям координат был равный. Касательные по таким полярам можно проводить. Углы атаки определятся верно, но вектор окружной скорости правильно не провести и величину его не измерить). Полученную точку снесем на правый график и получим альфа равный 9 градусам. Для желобков этот угол будет еще больше. Если же ветряк проектировать быстроходный с Z = 9, то угол альфа будет близок к рекомендуему Пиготом, в районе 6 градусов.

До сих пор мы говорили о кончике лопасти. В других сечениях лопасти, которые движутся медленнее, будут другими исходные данные. Другой коэффициент Re. Каждое сечение надо считать по своим полярам. В этом сложность…

В Вашем переводе

ЧИСЛО РЕЙНОЛЬДСА = 68 500 х ДЛИНА ХОРДЫ (м) х ИСТИННАЯ СКОРОСТЬ (м/с)
Если D = 2м и Z = 5 и V = 5 м/ c, то Re = 120 000
Если D = 2м это диаметр? И как Вы получили 120000? Где хорда?

Истинная скорость зависит от скороси автомобиля или от скорости лопастей, а не от боковой скорости ветра. Если ветер 5 м/с, то окружная скорость 25 м/с. Скорость ветра в плоскости колеса меньше чем на подлете к ветряку – 3,3 м/с. Прибавляем 3,3 + 25 = 25,2 м/с По правилу сложения вектроров. (треугольника). Хорда равна 7см, которую Хью сделал стандартом по умолчанию. Спасибо, что заметили. Исправлю.

как по графику из программы Profili правильно выбрать угол атаки?

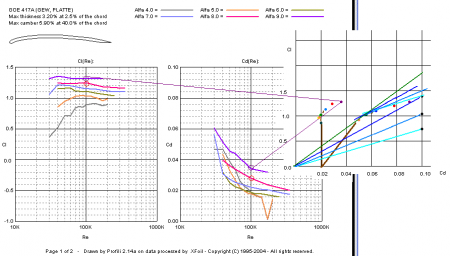
По-моему в программе Profili есть возможность построить график Cy(Cx), т.е. поляру? Я нарисовал, как можно построить поляру для 100 kRe из тех графиков, что приводите Вы. Рис.1. Далее добавляем на поляру индуктивное сопротивление. Индуктивное сопротивление – это добавочное лобовое сопротивление при коротких лопастях.

Cxi = Су²/(3,14лямбда)

где удлинение Лямбда = 0,7R/b
R – это радиус ветряка
b – средняя хорда лопасти

В начале расчета хорда неизвестна, поэтому надо ею задаться, а дальше методом последовательного приближения стыковать с другими результатами вычисления.

Зададимся удлинением равным 10,
Тогда при Cy = 1,3 (фиолетовая точка) Cxi = 0,054
при Cy = 1,0 (оранжевая точка) Cxi = 0,032
Сдвигаем фиолетовую точку вправо на 0,054. Было 0,035, стало 0, 09 И.Т.Д.

Из поляры профиля мы получили поляру лопасти.

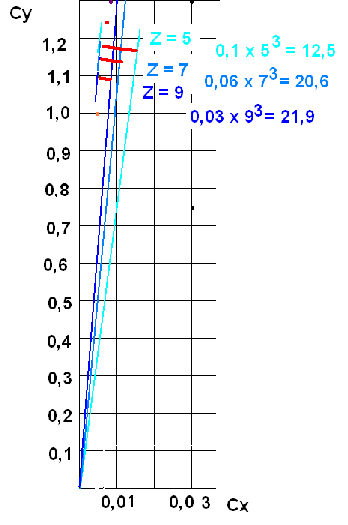
Проводим скоростные прямые при Z = 5, Z = 7, Z = 9.

Это делается так. Возьмем Сх = 0,1, тогда Cy = 1,5ZCx = 1,5*5*0,1 = 0,75 и из начала координат проводим к этим точкам линии

Теперь перенесем скоростные прямые вверх до касания с полярой. Получим углы атаки ПРОФИЛЯ.

Z = 5, альфа профиля равно 7,5 градусов
Z = 7, альфа профиля равно 7 градусов
Z = 9 альфа профиля равно 6 градусов

Угол атаки лопасти будет больше угла атаки профиля на величину

57,3Cy/(3,14лямбда)

Z = 5, альфа лопасти равно 7,5 + 2,3 = 9,8 градуса
Z = 7, альфа лопасти равно 7 + 2 = 9 градусов
Z = 9, альфа лопасти равно 6 + 1,9 = 7,9 градуса

Фетишизировать с этими цифрами не надо. Они дают понимание что на что влияет. Обратите внимание здесь вот на что. Пигот дает рекомендацию принять угол альфа в 4 или 5 градусов. Он исходит из идеального случая бесконечно длинной лопасти (профиля). Здесь по расчету с учетом индуктивных потерь получается от 8 до 10 градусов.

Теперь посчитаем быстроходность разноса.

Для этого проведем зеленую касательную. Максимально возможную скоростную прямую. И по какой-нибудь точке на ней Сх = 0,1 Cy = 1,8 найдем Z = 0, 67*1,8/0,1 = 12 Это, правда, не быстроходность разноса, но я не буду углубляться в этот вопрос.

Помните, Александр Николаевич считал качество профиля равное 30 – 60 Реальное качество лопасти получилось 1,8/0,1 = 18.

Какую быстроходность из подсчитанных можно взять? Обычно рабочая быстроходность равна примерно половине максимальной. Т.е. 6. Дальше начинаются нудные расчеты. Мы получили данные
Z = 6
Сy = 1,1
Cx = 0,02
альфа = 9,5 градусов
Re = 100 000

Рассчитываем по ним хорду, по полученной хорде уточняем число Re, на котором на самом деле кончик крыла работает. И для полученного уточненного значения Re и b строим новую поляру и вычисляем все по-новому.

За пару таких итераций получим конечный результат для Z = 6 или для другого Z, которым задались. Слишком высокий Z брать нельзя. Крыло не будет работать выше максимальной быстроходности, на которое оно способно. Расчеты покажут это, они попросту не будут сходиться в одну точку.

Если все же хочется получить максисмальную рабочую быстроходность, придется строить еще один график. График Cy(Cx) надо построить в одинаковом масштабе осей.

На этом графике очень трудно проводить касательные для разных скоростных прямых. поэтому точки касания надо взять с предыдущего графика. От точек касания надо провести красные отрезки к своим скоростным прямым. Красные отрезки – это коэффициент окружной силы Сокр.. Теперь каждый отрезок надо измерить линейкой, определить его величину по масштабу осей координат и умножить на куб своей быстроходности. Максимум получился при БКЛ 9. На самом деле мы пропустили промежуточные значения и максимум будет при БКЛ 8,5.

Дальше та же процедура. Считаем ширину лопасти. Проверяем, то ли число Рейнольдса мы взяли в качестве исходного. Пересчитываем….

И получаем, наконец, одну только точку на конце лопасти. Затем переходим к следующему сечению 0,9 R и для него считаем все тоже. Самое веселое будет, если внутренние сечения не пойдут при рассчитанной быстрохдности кончика и придется все начинать сначала. Надо программочку писать…

Что тут надо заметить. Если будет повышенная шероховатость, то быстроходность здорово упадет. Если будет отклонения геометрии профиля, результаты вообще могут быть катастрофическими. До двухкратного снижения быстроходности. Плюс неточности расчета. Кое-что я ввел в расчет «на глаз» предупреждаю сразу. Но не пугайтесь, в любом случае точность по сравнению с простыми расчетами намного повысилась. Кроме того, нужны достоверные поляры и достоверные поляры не просто одиночных крыльев, а решеток, как это делается в расчете турбин. Поэтому данные расчеты дают понятие, куда можно двигаться, чтобы приблизиться к желаемому результату.

По одной прикидке мы получили Z = 6, по другой – 8,5. Реальность будет в этих пределах. Конкретную величину может дать только опыт.

С уважением,
Михаил Николаевич